Raqcoin研究报告报告下载
Author:GF 欢迎转载但请保留作者姓名
摘要:
1.比特币为代表的几乎所有加密货币区块链系统都使用了“椭圆曲线ECC函数”数字签名为系统提供非对称加密。
2.1994年美国数学家Peter Shor在数学层面证明利用量子计算可以有效破解ECC函数,并发明了SHOR算法用以破解。
3.2001 年,IBM的一个小组展示了SHOR算法的实例,使用核磁共振的量子计算机,以及7个量子位元,将15质因数分解成3×5。从而在实践中论证SHOR算法破解ECC是可行的。
4.2016年美国NIST全球征选抗量子算法以抵抗日益临近的量子威胁,适合加密货币场景的多变量技术路线脱颖而出。
5.Raqcoin是多变量签名在区块链系统之加密货币实装应用的唯一产品。
6.2022年5月白宫公布第10号国家安防备忘录即NSM-10要求即日起全美国政府机构和全社会商业机构均参与升级到抗量子计算机破解算法,且将公布废弃包括椭圆曲线在内的经典密码学的时间表。2022年9月美国国家安全局NSA发布了CNSA(Commercial National Security Algorithm Suite)2.0,旨在将全美的安全信息系统升级到抗量子密码学以保护信息安全。因此官方主导的后量子密码学算法迁移大幕已经展开。
7.作为无主的加密货币区块链,向后量子密码学的迁移是必经之路,而不是可选之路,且因为无主特性,所以更加迫切。中心化机构的全面迁移已经浩浩荡荡的开始,去中心化的系统没理由拖沓不前。
8.每个新密码系统的发明创造到实装采用都需要10年到20年的时间,7年以来,这些最终站在NIST淘汰赛的候选者每一天都在遭受其它密码学专家团队的暴力破解,只有长期屹立不倒的算法才值得信任。未来一定有团队在NIST淘汰赛外宣称发明了新抗量子算法。但是这种不经过淘汰赛检验的算法是不可靠的,实践才是检验真理的唯一标准。倘若未来比特币用这种未经检测的算法进行改造,将承担巨大的风险。
关键词:椭圆曲线 Ellipse Curve;后量子密码学 PQC;美国国家技术标准局 NIST;美国国家安防备忘录10号 NSM-10;多标量数字签名 Multivariate;Raqcoin热矿币
行业技术发展的背景
椭圆曲线密码学(Elliptic Curve Cryptography,缩写:ECC)是一种基于椭圆曲线数学的公开密钥加密演算法。椭圆曲线在密码学中的使用是在1985年由Neal Koblitz和Victor Miller分别独立提出的。椭圆曲线密码学的演算法是在2004年至2005年开始广泛应用。2009年1月,比特币诞生。在比特币的内部结构中创始人中本聪使用了公钥密码学-非对称加密算法。他具体采用的就是椭圆曲线ECC函数方程作为数字签名算法,而之后的几乎所有加密货币的数字签名都采用的是椭圆曲线ECC这一技术。
在1994年,美国计算机科学家Peter Shor在贝尔实验室的内部研讨会上,提出了一个新的证明,表明量子系统能够比经典计算机更快地解决一个特定的问题。这个问题被称为离散对数问题,用经典计算机的方法是无法解决的,因此离散对数在当时成为了少数安全系统的基础。RSA与ECC都基于这一特定问题理论被制造出来的密码学算法。 Shor算法的发明使得在数学理论层面将椭圆曲线ECC和RSA的算法计算的破解复杂度(O)大幅降低。Peter Shor于2022年9月23日,荣获“2023年科学突破奖”(基础物理学突破奖)。[1]
时间来到2001年,IBM分别在5位NMR量子计算机、7位NMR量子计算机上成功运行了Shor量子算法,成功将21分解为3和7,将15分解为3和5,这标志着人类首次在硬件上实现Shor量子算法,从而在实践层面证明了量子算力与Shor算法合并使用对传统公钥密码学的威胁真实存在。[2]
……The simplest meaningful instance of Shor's Algorithm is finding the factors of the number 15, which requires a seven-qubit quantum computer. IBM chemists designed and made a new molecule that has seven nuclear spins -- the nuclei of five fluorine and two carbon atoms -- which can interact with each other as qubits, be programmed by radio frequency pulses and be detected by nuclear magnetic resonance (NMR) instruments similar to those commonly used in hospitals and chemistry labs.……
笔者按:前文提及椭圆曲线在2004至2005年被大规模应用,而1994年和2001年理论层面就破解了椭圆曲线密码学这件事在逻辑上并不冲突。因为算力的限制,人们认为离可用于实际破解现实密码学的量子计算机的发明还很遥远,所以并不担心椭圆曲线在短时间内被真正破解,在当下正常使用无需担心。
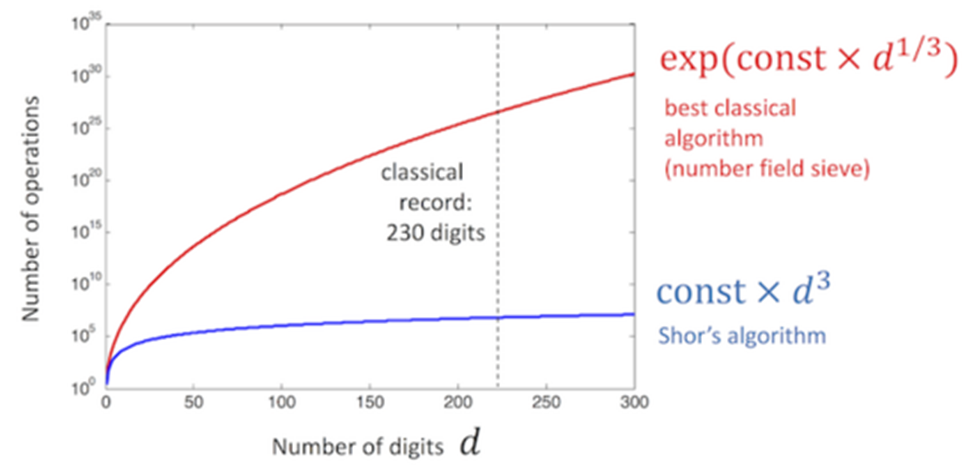
上图是经典大数分解和秀尔算法的复杂度对比
鉴于量子威胁的日益临近,美国国家技术标准局NIST在2016年发起了全球范围内征集抗量子计算破解算法的项目,目的是对新算法进行标准化,并为之后各个领域的密码学算法全面升级做好准备[3]。抗量子破解算法,也称后量子密码学(PQC)。从形式上划分,PQC分成公钥加密和数字签名。和加密货币有关的是数字签名算法。经过8年时间,3轮淘汰赛,截止到第3轮,数字签名类最终3个技术路线被确定,它们是格Lattice签名,哈希Hash函数签名,多变量Multivarite签名。其中格签名Crystal-Delithium,格签名Crystal-Falcon,多变量签名Rainbow被列为正选算法。哈希签名SPHINCS+为备选算法。[4]截止当前2024年2月,NIST披露尚无数字签名的标准算法完全胜选,未来还将举行第四轮的竞选[5
量子威胁的正确理解
人们普遍认为,只有在量子计算机发明并被媒体广泛报道后,对传统的密码学的威胁才会到来。但他们并没有用博弈的角度思考量子威胁这一问题。因为对密码学的攻击破解往往都不会是公开的炫耀,而是隐蔽的盗取,偷偷获得被密码保护下的信息,在对手不知情的情况下拥有信息差,使自己处于有利位置。其中最经典的案例莫过于第二次世界大战期间英国科学家图灵团队对纳粹德国Enigma密码器的破译,英国人在破解了Enigma密码器后没有公开炫耀自己的成就,那样会使得德国改变自己的加密策略,而是暗暗获取德国的军事情报,将计就计。当德国计划伦敦大轰炸时,其实英国早已知晓,但是为了不让德国起疑,不能疏散全部市民,让德国轰炸机来炸一座空城。破译Enigma密码器的这一事件要等到50年后的1990s年代才最终解密,让世人知晓原来二战时期的隐秘战线原来还有这样的故事。[6]因此攻击型量子计算机,特别是军事用途的量子计算机(CRQC)的发明很可能不会有任何媒体报道。
此外,加密期与解密期是一个组织对机密档案管理的重要方法。机密档案在加密期不公之于众,只有在解密期到来之际才可以公布。解密期的设定被认为是当公众在该时点知晓档案信息也不会对组织安全产生不利影响。而量子威胁对现代组织的影响还可以会是这样的,当一个机密档案还处于加密期,假设离解密还有50年时间。那么攻击者可以先将被加密的档案数据包盗取下载转移到自己的存储之中,攻击者当下确实没有量子计算机可以破解该密码,传统的算法破解该数据更是天方夜谭。但是大国博弈,科技是前沿,也许20年后随着科技的发展量子计算机就被发明,甚至已经高度应用。这样一来,20年后攻击者就有可能破解该数据包,而解密期要等到50年以后,这意味着攻击者可能会提前30年解密这些数据。这样的情景肯定会造成极大的泄密隐患。
当然有鉴于此,未雨绸缪才是应对良策,在一个黑暗森林的博弈对局中获取优势。美国国家安防备忘录NSM-10(于2022年5月4日发布)明确了密码学从传统到后量子密码学PQC的迁移路线和2035年全美各机构全面迁移到抗量子密码学算法的期限。而且在Section3-c-vii中明确提及,未来将公布易受量子攻击算法的弃用时间表。
……(vii)Within 90 days of the release of the first set of NIST standards for quantum-resistant cryptography referenced in subsection 3(a) of this memorandum, and on an annual basis thereafter, as needed, the Secretary of Commerce, through the Director of NIST, shall release a proposed timeline for the deprecation of quantum-vulnerable cryptography in standards, with the goal of moving the maximum number of systems off quantum-vulnerable cryptography within a decade of the publication of the initial set of standards. The Director of NIST shall work with the appropriate technical standards bodies to encourage interoperability of commercial cryptographic approaches.……[7]
(椭圆曲线函数数字签名ECC被归类为易受攻击的算法之内)。
在2022年9月美国国家安全局发布了CNSA(Commercial National Security Algorithm Suite)2.0,旨在全美安全系统升级到PQC算法,并且在数字签名领域推荐使用双锂电池 CRYSTALS-Dilithium 数字签名,取代了之前的椭圆曲线ECC签名。并且要求全部的合作企业(包括浏览器、云服务、操作系统、网络设备硬件)必须升级到PQC,并给出时间表。[8]

当下美国为代表的中心化组织已经开始动员全美各个大型机构全面迁移到PQC,并已经有完整的计划,那么去中心化的加密货币该何去何从?椭圆曲线在实装应用了20年之后,面对各个国家,各个大型科技公司在量子计算研发上面的布局发力,面对海量资本向量子霸权的押注,已经开始显露疲态。加密货币这种椭圆曲线保护下的无主产品找到新的庇护所才是重中之重。前文提及NIST全球征选的后量子密码学将会是加密货币升级指明方向。
后量子密码学PQC与加密货币的关系
公钥密钥密码学(Public-key cryptography)也称非对称式密码学(Asymmetric cryptography)是密码学的一种演算法,它需要两个密钥,一个是公开密钥,另一个是私有密钥;公钥用作加密,私钥则用作解密。使用公钥把明文加密后所得的密文,只能用相对应的私钥才能解密并得到原本的明文,最初用来加密的公钥不能用作解密。由于加密和解密需要两个不同的密钥,故被称为非对称加密;不同于加密和解密都使用同一个密钥的对称加密。公钥可以公开,可任意向外发布;私钥不可以公开,必须由用户自行严格秘密保管,绝不透过任何途径向任何人提供,也不会透露给被信任的要通讯的另一方。
而在信息传输的过程中又需要数字签名技术。数字签名(又称公钥数字签名)是只有信息的发送者才能产生的别人无法伪造的一段数字串,这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。它是一种类似写在纸上的普通的物理签名,但是在使用了公钥加密领域的技术来实现的,用于鉴别数字信息的方法。一套数字签名通常定义两种互补的运算,一个用于签名,另一个用于验证。数字签名是非对称密钥加密技术与数字摘要技术的应用。
在加密货币里面使用的都是数字签名类公钥密码。而数字签名在后量子密码学PQC之中有三个技术路线,分别是基于格Lattice的数字签名,基于哈希Hash的数字签名,基于多变量Multivariate的数字签名。考量数字签名应用场景的指标有三个:私钥长度(size),公钥长度(size),签名长度(size)。私钥储存在本地,用于解密计算,因此,对于私钥的大小没有特别的要求,而公钥和签名都需要发送至通讯网络,所以对大小的要求的限制非常多,想象一下微信发送大容量视频速度是不是很慢?所以最好的公钥和签名是长度又小,安全又高的。如下图所示
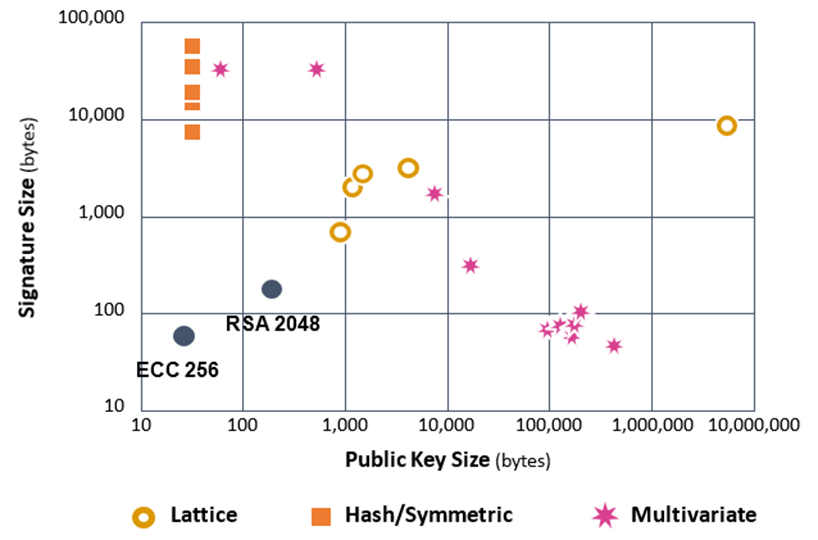
从图中可以看到,ECC256在矩阵图的最左下方,意味着签名和公钥都很小,均不到100Bytes。这也就是为什么当初中本聪选择ECC作为比特币的基石加密算法的原因,小巧便捷易于传输,太大的Size会造成拥堵。
在量子威胁之下,ECC和RSA算法肯定是不安全了,即便它们有小巧的优势。那么只能在PQC算法里面选择。哈希签名的公钥不大,但是签名非常大。多变量签名的签名不大,但是公钥非常大。而格签名在两者之间,而签名长度和公钥长度也要比ECC大20倍以上。也就是说抗量子密码学PQC的几种方案都存在长度的问题,尽管算法方程式的参数可以调整,可数量级的大小不会改变,否则将失去安全性。
当下的PQC方案是NIST征集了7年时间才产生的技术路线,大部分候选算法在第一轮因为安全问题就被淘汰掉了。那么加密货币未来的抗量子密码升级方案也只能在这几种方案里面选,而没有无限的选择。因此算法就是这样了,那么一定是要在工程结构上扬长避短,不让PQC的缺点影响到性能。
下面我们要重新温习一下非对称加密的一些知识。数字签名是发送者身份和行为的确认,代表了该项操作是由那个私钥的持有人进行的,公钥用于加密信息,并向全网广播,是公开的。这里面涉及到一个具体的工程学问题,公钥虽然每次都广播,但是每次都是固定的,因为公钥是私钥通过一个单向函数生成的,是函数的唯一解。而签名则不同,签名函数里面有2个变量,分别是私钥和消息,每次发送的消息不同,所以数字签名每次都不一样。那么基于这个特性,可以在PQC的结构中寻求一定的优化,以起到扬长避短之功效。既然公钥是永远不变的,那么公钥可以做一个邮政编码化,也就是将地址信息进行发送,因为地址是公钥通过特定函数生成的,它一样具有高度的唯一性和抗碰撞性。地址可以看作是公钥的索引,那么这个问题就变成了,加密货币在使用过程之中,一个地址只需要广播一次公钥即可,以后的转账等交易,无需每次都广播公钥,只需要广播地址用于查询就可以,这样就可以一定程度的规避公钥过大的问题。
在采用工作量证明POW共识机制的加密货币中,对签名长度的要求更加敏感,因为节点众多且分布广泛,一旦签名长度超过系统的处理能力时,转账系统可能会出现大规模拥堵。固定节点或者少量节点的质押量证明POS有可能可以使用其他的数字签名。最早且市值最大的加密货币比特币Bitcoin中采用的是POW机制。
那么重新审视上面的图例,如果顺着这条路线思考,最可能用于POW加密货币场景升级的技术路线就是多变量签名Multivariate,因为它具有和ECC一样数量级的签名大小,和一个非常大的公钥,而大公钥的缺点可以通过邮政编码化的技术进行优化,使它的缺点降低到可用范围内。
多变量签名
彩虹签名Rainbow是多变量签名的代表,根据官方的介绍,彩虹签名于2004年发明,创造者是Jintai Ding和Dieter Schmidt,它构筑在以不平衡油醋混合签名UOV方案上,后者的发明人是Jacques Patarin。彩虹签名于2020年7月22日进入NIST遴选算法的最终名单(Finalist)。它的理论基础是基于解决一个二次多项式函数的NP问题,这个背后蕴含着重要的数学思想——代数几何学。从结果上看,该签名的长度仅仅528个字节,比其他的PQC方案都要短小许多。不平衡油醋方案是多变量签名的重要基础,许多签名都是由不平衡油醋改进而来。[9]
引述Google Patent上面的原文:…J.Patarin设计了一个新方案,称为“油与醋”,用于计算不对称签字。它很简单,可以很快地计算(在秘密和公共密钥两种情况下)而在智能卡实施中需要很小的RAM。此方案的想法包含将二次方程隐藏于有限域K中n个称为“油”的未知数和v=n个称为“醋”的未知数内。此初始方案由A.Kipnis和A.Shamir提出。在此论文中,我们研究初始方案的某些很简单的变动,其中v>n(而不是v=n)。这些方案称为“不平衡油与醋”(UOV),因为我们具有比“油”未知数更多的“醋”未知数。我们证明,当v≌n时,可以扩充的概念,但当例如v≥2n时,该方案的安全性仍然是一个悬案。此外,当v≌n2/2时,该方案的安全性完全相当于(如果我们接受一个很自然但没有证明的特性的话)解n2/2个未知数的n个二次方程的随机组(没有秘密信息)的问题。然而,我们显示了(在特征2的情形中)当v≥2n时,求解通常是容易的。然后我们将看到,把油与醋的想法和HFE方案综合是容易的。现在从实际的和理论的观点两者来看,所得的称为HFEV的方案也都是很有趣的。UOV签字的长度可以短至192位而对于HFEV则可以短至80位。…[10]
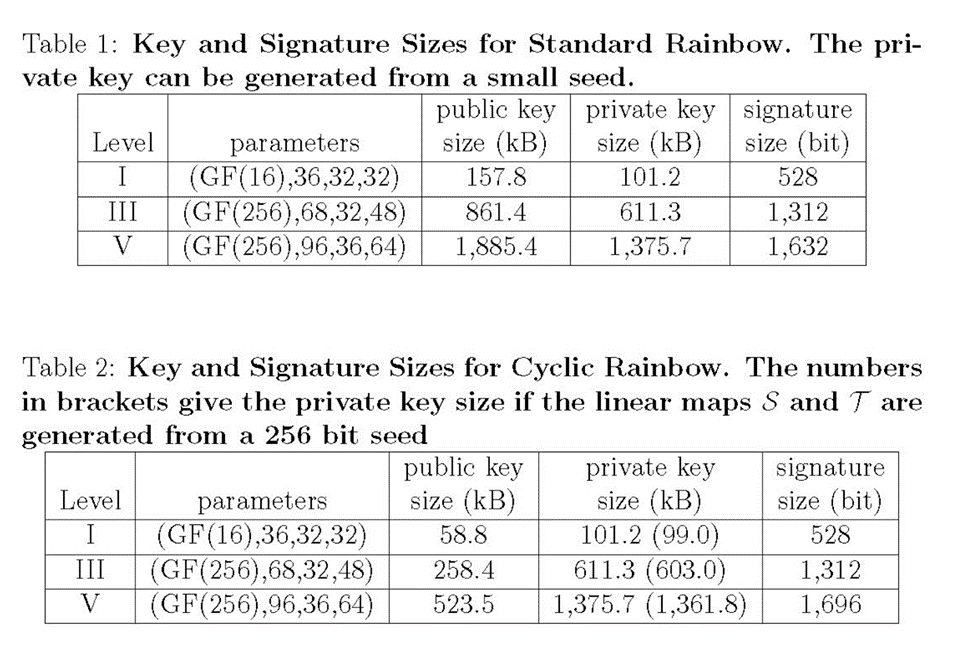
上图是彩虹签名的私钥,公钥,签名的长度表格[8]
Raqcoin介绍
Raqcoin的前身名为ABCMint,在2018年6月18日启动,后于2022年经社区投票表决改名Raqcoin,中文名:热矿币。是当前唯一实装了多变量数字签名的加密货币,至今稳定运行了已经近6年,采用了POW的共识机制,它是一种类比特币形式的加密货币,实现价值存储,数字黄金的功能。正常转账速度流畅,得益于它的公钥邮政编码化解决方案和多变量的短签名特性。在Raqcoin创造之初,数学结构由彩虹签名的作者提供,代码程序由匿名团队创建,所有代码全部开源。
在2022年1月,一个密码学团队攻击了安全等级为1的彩虹签名。随后Raqcoin将算法全面升级到更高等级,消解了该项攻击。后量子密码学非常前沿,这也是一场产品与算法的整合实验。因此当下的Raqcoin加密货币,每一组助记词可以生成7个私钥对应的7个地址,每个地址被不同等级的多变量函数保护。用户可以自己选择将加密货币储存在哪个等级的签名之下。安全等级低的地址转账手续费会比安全等级高的手续费低。特别要指出的是安全等级低并不意味着存在被轻易破解的风险,在计算机领域对于安全等级的定量描述是复杂度函数O,举例来说就是,低安全等级的密码系统在某一个计算效率下,需要500年破解,高安全等级的密码系统在同样的计算效率下需要5亿年破解。无论是500年还是5亿年,在现实实践当中都是可用的,都符合了安全标准。
比特币的挖矿是求解哈希函数,目前比特币矿工需要使用专业的ASIC矿机进行哈希计算以求解目标值。这样会增加挖矿的门槛,使得个人设备被完全排除在挖矿之外,不利于去中心化。Raqcoin采用的是求解多项式函数,平均每10分钟出一个区块,当挖矿算力变高或变低时,挖矿难度自动调节以适应出块的平均时间。理论上采用笔记本电脑的显卡就可以挖矿,一定程度上更加公平。Raqcoin的产出总量是2,147,483,647,是比特币总量的约100倍。全部挖完需要大概90年。每隔5年左右产量下降,下降比例是前一次的73.5%。前8年大致会产出总供应量的50%。当前2024年处于第一次挖矿减半之后,每一个新区块奖励矿工1884个Raqcoin,总供应量为8亿个Raqcoin。
目前Raqcoin的钱包还是独立钱包,并没有植入在主流的手机钱包当中。Raqcoin钱包分成两种,一种是PC端的全节点钱包,另一种是手机端的轻节点钱包。无论哪一种钱包都是去中心化的,私钥需由资产主人亲自保管,遗失私钥即资产永久丢失。
后记
后量子密码学非常前沿,从各项算法的发明时间上看,基本都在20年以上的时间,密码安全不是一朝一夕可以知晓证明的,路遥方知马力。特别是这一次NIST举办了一场空前的选拔赛,全世界顶尖的大学密码学团队悉数提交了自己的密码学方案。从结果上看,2017年12月21日,第一轮比赛时,一共有69个PQC算法参赛,到2019年1月30日,第二轮比赛时,只有26个算法在列。另外的43种算法全部被破解淘汰出局,有的算法24小时就被其他专业团队破解。因此可以说竞争十分残酷,在密码学领域被破解的算法一文不值,团队多年的心血之作全部归零。即便如此依然不能有效证明剩下的26个算法是安全的。于是2020年7月22日,第三轮比赛开始,台上还剩下15个算法。又有11个算法被破解淘汰出局,从开赛到这时已经历三年时间。那在列15个算法就一定安全了吗?不是的,比赛还需要继续进行,这是一场马拉松长跑。破解密码学并不是数学考试,要求答题者在短时间完成试卷。它要给予破解者足够长的思考时间,严格说是特别特别特别长。有可能破解者今年没想到破解之法,明年想出来了,所以绝不能草率的结束比赛。截止到今天——2024年4月,PQC中的密钥交换领域的算法已经被标准化推荐了,而数字签名依然没有最终答案,前文提到了,未来的需求场景不同,适应的数字签名也不相同,不容易标准化,唯一化。所以可以看出选拔之艰难。
可以想象的是,当下依然有众多的投资者对比特币升级到PQC保持着盲目乐观的态度。要么认为现在离Q-Day还很遥远,因此量子威胁不足为虑。要么认为即便Q-Day到来,有很多的解决方案,如同超市里琳琅满目的商品待客挑选。要么认为当Q-Day临近,临时想办法发明一个就可以使用了。这些都是错误的认知。PQC可以选择的方案非常少,而多变量数字签名甚至可能是加密货币场景的唯一解法。
此外,也会有很多人对于这一次NIST长期淘汰赛的含金量重视不足。未来一定会有某团队宣称自己发明了新的PQC密码系统,但是这种未经淘汰赛检测过的密码学很可能有极大安全漏洞,想想NIST第一轮比赛到第二轮比赛的惨烈程度,提交者都是顶级大学或是科研院所的密码学团队,即便如此照样铩羽而归。前文还提到了现在还在列的算法的年龄都在20年以上,前10年或15年在实验室学术界讨论,后10年参与NIST遴选打榜,这是一个多么长期的记录。所以那些不经历长期淘汰赛检测的算法真的能保护背后的数据吗?你发明个3-5年,然后产品测试上运行个6个月,你就宣称自己的算法能抗量子计算了?这些都是那些乐观派要扪心自问的。
以上全文框架逻辑数据,请各位读者自行检索验证。下方有溯源引用链接。
最后,Do your own research,不要简单轻信依赖本文逻辑,自己根据检索资料论证结果。
附录:
以下是Raqcoin有关的详细资料链接
Raqcoin浏览器: https://abcscan.io
Raqcoin源代码: https://github.com/abcmint/abcmint
Raqcoin使用教学网站:http://www.raqcoin.club/
[1] Peter Shor’s Wiki : https://en.wikipedia.org/wiki/Peter_Shor#External_links
[2] IBM's Test-Tube Quantum Computer Makes History; First Demonstration Of Shor's Historic Factoring Algorithm https://www.sciencedaily.com/releases/2001/12/011220081620.htm
[3] NIST initiated a process to solicit, evaluate, and standardize one or more quantum-resistant public-key cryptographic algorithms. Full details can be found in the Post-Quantum Cryptography Standardization page https://csrc.nist.gov/projects/post-quantum-cryptography/post-quantum-cryptography-standardization
[4] Official comments on the Third Round Candidate Algorithms should be submitted using the "Submit Comment" link for the appropriate algorithm. https://csrc.nist.gov/Projects/post-quantum-cryptography/post-quantum-cryptography-standardization/round-3-submissions
[5] NIST announced that the PQC standardization process is continuing with a fourth round, with the following KEMs still under consideration: BIKE, Classic McEliece, HQC, and SIKE. However, there are no remaining digital signature candidates under consideration. https://csrc.nist.gov/projects/pqc-dig-sig
[6] Enigma密码机的维基百科:https://zh.wikipedia.org/zh-hans/恩尼格玛密码机#恩尼格玛的破译
[8] https://media.defense.gov/2022/Sep/07/2003071834/-1/-1/0/CSA_CNSA_2.0_ALGORITHMS_.PDF
[9] Rainbow Website: https://www.pqcrainbow.org
[10] 谷歌专利网:https://patents.google.com/patent/CN1314040A/zh
