① ECC椭圆曲线非对称加密原理
比特币Bitcoin使用了 secp256k1这条特殊的椭圆曲线:
一、阿贝尔群
封闭性:如果a和b都是 的成员,那么a+b也是 的成员;
结合律:(a + b) + c = a + (b + c);
单位元:a+0=0+a=a,0就是单位元;
逆元:对于任意值a必定存在b,使得a+b=0。
二、椭圆曲线的加法
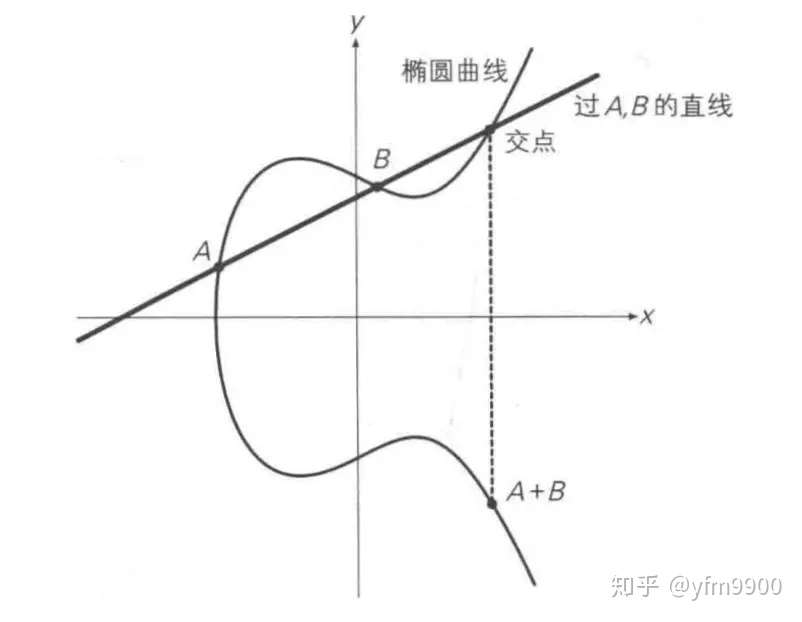
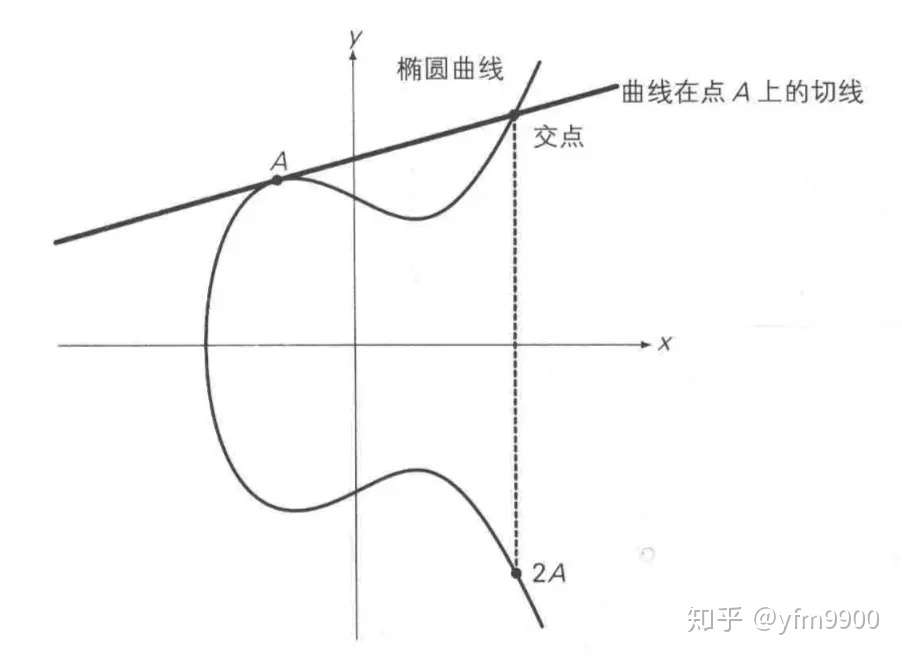
上述方法无法解释A + A,即两点重合的情况,因此在这种情况下,将椭圆曲线在A点的切线,与椭圆曲线的交点,交点关于x轴对称位置的点,定义为A + A,即2A,即为二倍运算。
同余就是有相同的余数,两个整数 a、 b,若它们除以正整数 m所得的余数相等,则称 a, b对于模m同余。
五、有限域
在模7乘法中:
七、数学解释
针对曲线Ep(a,b)表示为
该曲线关于x轴对称。选择两个满足下列条件的小于p(p为素数)的非负整数a、b,要求满足以下条件
的负元是
2、有限域的加法,
3、斜率计算(P=Q即要计算P点切线,需要求导)
该公式可以自己推导,为了方便理解,可以套用以上公式,解决以下例题。
解:1) 的负元是
3) ,
,因为
,5的乘法逆元为14,故k=6。
故
的坐标为
设私钥、公钥分别为d、Q,即Q = dG,其中G为基点,椭圆曲线上的已知G和dG,求d是非常困难的,也就是说已知公钥和基点,想要算出私钥是非常困难的。
公钥加密:选择随机数r,将消息M生成密文C,该密文是一个点对,C = {rG, M+rQ},其中Q为公钥。
私钥解密:M + rQ - d(rG) = M + r(dG) - d(rG) = M,其中d、Q分别为私钥、公钥。
椭圆曲线签名算法(ECDSA)。设私钥、公钥分别为d、Q,即Q = dG,其中G为基点。
选择随机数r,计算点rG(x, y)。
根据随机数r、消息M的哈希h、私钥d,计算s = (h + dx)/r。
将消息M、和签名{rG, s}发给接收方。
接收方收到消息M、以及签名{rG=(x,y), s}。
根据消息求哈希h。
使用发送方公钥Q计算:hG/s + xQ/s,并与rG比较,如相等即验签成功。
原理:hG/s + xQ/s = hG/s + x(dG)/s = (h+xd)G/s = r(h+xd)G / (h+dx) = rG
假设要签名的消息是一个字符串:“Hello World!”。DSA签名的第一个步骤是对待签名的消息生成一个消息摘要,不同的签名算法使用不同的消息摘要算法,而ECDSA256使用SHA256生成256比特的摘要。
产生一个随机数k
利用随机数k,计算出两个大数r和s。将r和s拼在一起就构成了对消息摘要的签名。
这里需要注意的是,因为随机数k的存在,对于同一条消息,使用同一个算法,产生的签名是不一样的。从函数的角度来理解,签名函数对同样的输入会产生不同的输出。因为函数内部会将随机值混入签名的过程。
关于验证过程,这里不讨论它的算法细节。从宏观上看,消息的接收方从签名中分离出r和s,然后利用公开的密钥信息和s计算出r。如果计算出的r和接收到的r值相同,则表示验证成功,否则,表示验证失败。
# -*- coding:utf-8 -*-
def get_inverse(value, p):
"""
求逆元
:param value: 待求逆元的值
:param p: 模数
"""
for i in range(1, p):
if (i * value) % p == 1:
return i
return -1
def get_gcd(value1, value2):
"""
辗转相除法求最大公约数
:param value1:
:param value2:
"""
if value2 == 0:
return value1
else:
return get_gcd(value2, value1 % value2)
def get_PaddQ(x1, y1, x2, y2, a, p):
"""
计算P+Q
:param x1: P点横坐标
:param y1: P点纵坐标
:param x2: Q点横坐标
:param y2: Q点纵坐标
:param a: 曲线参数
:param p: 曲线模数
"""
flag = 1 # 定义符号位(+/-)
# 如果P=Q,斜率k=(3x^2+a)/2y mod p
if x1 == x2 and y1 == y2:
member = 3 * (x1 ** 2) + a # 分子
denominator = 2 * y1 # 分母
# 如果P≠Q, 斜率k=(y2-y1)/(x2-x1) mod p
else:
member = y2 - y1
denominator = x2 - x1
if member * denominator < 0: flag = 0 # 表示负数 member = abs(member) denominator = abs(denominator) # 化简分子分母 gcd = get_gcd(member, denominator) # 最大公约数 member = member // gcd denominator = denominator // gcd # 求分母的逆元 inverse_deno = get_inverse(denominator, p) # 求斜率 k = (member * inverse_deno) if flag == 0: k = -k k = k % p # 计算P+Q=(x3,y3) x3 = (k ** 2 - x1 - x2) % p y3 = (k * (x1 - x3) - y1) % p return x3, y3 def get_order(x0, y0, a, b, p): """ 计算椭圆曲线的阶 """ x1 = x0 # -P的横坐标 y1 = (-1 * y0) % p # -P的纵坐标 temp_x = x0 temp_y = y0 n = 1 while True: n += 1 # 累加P,得到n*P=0∞ xp, yp = get_PaddQ(temp_x, temp_y, x0, y0, a, p) # 如果(xp,yp)==-P,即(xp,yp)+P=0∞,此时n+1为阶数 if xp == x1 and yp == y1: return n + 1 temp_x = xp temp_y = yp def get_dot(x0, a, b, p): """ 计算P和-P """ y0 = -1 for i in range(p): # 满足适合加密的椭圆曲线条件,Ep(a,b),p为质数,x,y∈[0,p-1] if i ** 2 % p == (x0 ** 3 + a * x0 + b) % p: y0 = i break # 如果找不到合适的y0返回False if y0 == -1: return False # 计算-y x1 = x0 y1 = (-1 * y0) % p return x0, y0, x1, y1 def get_graph(a, b, p): """ 画出椭圆曲线散点图 """ xy = [] # 初始化二维数组 for i in range(p): xy.append(['-' for i in range(p)]) for i in range(p): value = get_dot(i, a, b, p) if value is not False: x0, y0, x1, y1 = value xy[x0][y0] = 1 xy[x1][y1] = 1 print('椭圆曲线散点图:') for i in range(p): temp = p - 1 - i if temp >= 10:
print(temp, end='')
else:
print(temp, end='')
# 输出具体坐标值
for j in range(p):
print(xy[j][temp], end='')
print()
print(' ', end='')
for i in range(p):
if i >= 10:
print(i, end='')
else:
print(i, end='')
print()
def get_nG(xG, yG, priv_key, a, p):
"""
计算nG
"""
temp_x = xG
temp_y = yG
while priv_key != 1:
temp_x, temp_y = get_PaddQ(temp_x, temp_y, xG, yG, a, p)
priv_key -= 1
return temp_x, temp_y
def get_KEY():
"""
生成公钥私钥
"""
# 选择曲线方程
while True:
a = int(input('输入椭圆曲线参数a(a>0)的值:'))
b = int(input('输入椭圆曲线参数b(b>0)的值:'))
p = int(input('输入椭圆曲线参数p(p为素数)的值:'))
# 满足曲线判别式
if (4 * (a ** 3) + 27 * (b ** 2)) % p == 0:
print('输入的参数有误,请重新输入!
')
else:
break
# 输出曲线散点图
get_graph(a, b, p)
# 选择基点G
print('在上图坐标系中选择基点G的坐标')
xG = int(input('横坐标xG:'))
yG = int(input('纵坐标yG:'))
# 获取曲线的阶
n = get_order(xG, yG, a, b, p)
# 生成私钥key,且key<n priv_key="int(input('输入私钥key(<%d):'" %="" n))="" #="" 生成公钥key="" xk,="" yk="get_nG(xG," yg,="" priv_key,="" a,="" p)="" return="" yk,="" b,="" p,="" n,="" xg,="" yg="" def="" encrypt(xg,="" n):="" """="" 加密="" k="int(input('输入一个整数k(<%d)用于计算kG和kQ:'" kgx,="" kgy="get_nG(xG," kg="" kqx,="" kqy="get_nG(xK," kq="" plain="input('输入需要加密的字符串:')" c="[]" print('密文为:',="" end="" )="" for="" char="" in="" plain:="" intchar="ord(char)" cipher="intchar" *="" kqx="" c.append([kgx,="" kgy,="" cipher])="" print('(%d,%d),%d'="" (kgx,="" cipher),="" print()="" decrypt(c,="" p):="" 解密="" chararr="" c:="" chararr[1],="" print(chr(chararr[2]="" kqx),="" if="" __name__="=" '__main__':="" n)="" p)
上一篇:没有了!
