背景详情

Shor算法在量子计算机上分解整数N的时间复杂度为 logNlogN，几乎是对已知最有效的经典因数分解算法的 ee 指数加速，这种加速有可能在量子计算机上中断如RSA的现代加密机制。

Shor算法要解决的主要问题是：给定一个整数N，找出它的质因数。即对一个给定的较大数 NN 在多项式时间内确定两个素因子 p1p1和 p2p2 满足 p1⋅p2=Np1⋅p2=N。 在介绍shor算法步骤之前，先介绍一些数论知识。

因此，Shor算法的核心在于，将大数分解的问题转化为找周期的问题（如下数论知识所示）。我们可以通过构造一个酉矩阵 Ux,N|j⟩|k⟩−>|j⟩∣∣xjkmodN⟩Ux,N|j⟩|k⟩−>|j⟩|xjkmodN⟩， 最终的结果满足 xr=1(modN)xr=1(modN)。

1. 选择一个任意的数字，比如 a=2a=2 (<15)

2. gcd(a,N)=gcd(2,15)=1gcd⁡(a,N)=gcd(2,15)=1

3. 找函数 f(x)=axmodNf(x)=axmodN 的周期，使得 f(x+r)=f(x)f(x+r)=f(x)

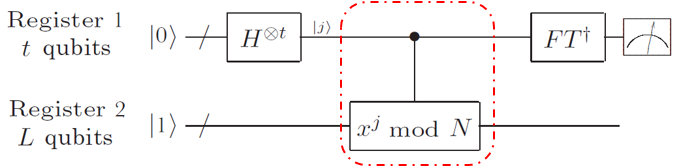
4. 通过量子电路图运算得到 r=4r=4

5. gcd(ar2+1,N)=gcd(5,15)=5gcd(ar2+1,N)=gcd(5,15)=5

6. gcd(ar2−1,N)=gcd(3,15)=5gcd(ar2−1,N)=gcd(3,15)=5

7. N=15N=15 分解得到的质数结果为 3 和 5，分解完成。

<p background-color:#fcfcfc;"="" style="padding: 0px; margin-top: 0px; margin-bottom: 10px; list-style: none; line-height: 25px; background-color: rgba(255, 255, 255, 0.5); font-family: "Microsoft YaHei"; white-space: normal; color: rgb(64, 64, 64); background-image: none !important; background-position: initial !important; background-size: initial !important; background-repeat: initial !important; background-attachment: initial !important; background-origin: initial !important; background-clip: initial !important;">Shor算法的量子电路如下图所示：